Quantitative microbial risk assessment of Vibrio parahaemolyticus foodborne illness of sea squirt (Halocynthia roretzi) in South Korea

Kang, Joohyun; Lee, Yewon; Choi, Yukyung; Kim, Sejeong; Ha, Jimyeong; Oh, Hyemin; Kim, Yujin; Seo, Yeongeun; Park, Eunyoung; Rhee, Min Suk; Lee, Heeyoung; Yoon, Yohan

doi:10.47853/FAS.2021.e8

Fish Aquat Sci 2021; 24(2):78-88

eISSN: 2234-1757

DOI: https://doi.org/10.47853/FAS.2021.e8

RESEARCH ARTICLE

Quantitative microbial risk assessment of Vibrio parahaemolyticus foodborne illness of sea squirt (Halocynthia roretzi) in South Korea

Joohyun Kang¹, Yewon Lee¹, Yukyung Choi², Sejeong Kim², Jimyeong Ha², Hyemin Oh², Yujin Kim¹, Yeongeun Seo¹, Eunyoung Park¹, Min Suk Rhee³, Heeyoung Lee⁴^,^*

, Yohan Yoon¹^,²^,^*

Author Information & Copyright ▼

¹Department of Food and Nutrition, Sookmyung Women’s University, Seoul 04310, Korea

²Risk Analysis Research Center, Sookmyung Women’s University, Seoul 04310, Korea

³Department of Biotechnology, College of Life Sciences and Biotechnology, Korea University, Seoul 02841, Korea

⁴Korea Food Research Institute, Wanju 55365, Korea

^*Corresponding author: Heeyoung Lee, Korea Food Research Institute, Wanju 55365, Korea, Tel: +82-63-219-9454, Fax: +82-63-219-9333, E-mail: hylee06@kfri.re.kr, ORCID: https://orcid.org/0000-0001-6115-9179

^*Corresponding author: Yohan Yoon, Department of Food and Nutrition, Sookmyung Women’s University, Seoul 04310, Korea, Tel: +82-2-2077-7585, Fax: +82-2-710-9479, E-mail: yyoon@sm.ac.kr, ORCID: https://orcid.org/0000-0002-4561-6218

Copyright © 2021 The Korean Society of Fisheries and Aquatic Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 24, 2020; Revised: Jan 26, 2021; Accepted: Jan 26, 2021

Published Online: Feb 28, 2021

Abstract

The annual consumption of fishery products, particularly sea squirt (Halocynthia roretzi), per person has steadily increased in South Korea. However, the quantitative risk of Vibrio parahaemolyticus following intake of sea squirt has not been analyzed. This study focuses on quantitative predictions of the probability of consuming sea squirt and getting of V. parahaemolyticus foodborne illness. The prevalence of V. parahaemolyticus in sea squirt was evaluated, and the time spent by sea squirt in transportation vehicles, market displays, and home refrigerators, in addition to the temperature of each of these, were recorded. The data were fitted to the @RISK program to obtain a probability distribution. Predictive models were developed to determine the fate of V. parahaemolyticus under distribution conditions. A simulation model was prepared based on experimental data, and a dose-response model for V. parahaemolyticus was prepared using data from literature to estimate infection risk. V. parahaemolyticus contamination was detected in 6 of 35 (17.1%) sea squirt samples. The daily consumption quantity of sea squirt was 62.14 g per person, and the consumption frequency was 0.28%. The average probability of V. parahaemolyticus foodborne illness following sea squirt consumption per person per day was 4.03 × 10⁻⁹. The objective of this study was to evaluate the risk of foodborne illness caused by Vibrio parahaemolyticus following sea squirt consumption in South Korea.

Keywords: Quantitative microbial risk assessment; Vibrio parahaemolyticus; Sea squirt; Halocynthia roretzi

Introduction

Fishery product consumption has increased steadily over the past 50 years as public awareness of healthy and diversified diets has increased (FAO, 2016). According to the Food and Agriculture Organization (FAO) of the United Nations, global food fish consumption per capita increased from 9 kg in 1961 to 20.2 kg in 2015 (FAO, 2018). Per capita fish consumption is expected to increase from 20.5 kg in 2015–17 to 21.3 kg by 2027 (OECD & FAO, 2018). According to statistics in Korea, the annual consumption of fishery products per person increased from 56.5 kg in 2007 to 65.9 kg in 2017 (KOSTAT, 2019). In particular, the consumption of raw sea squirt has gradually increased in South Korea (Kim et al., 2013).

Vibrio parahaemolyticus (V. parahaemolyticus) is a gram-negative, aerobic, halophilic, and non-spore forming rod bacterium that is frequently isolated from river and ocean areas (FDA, 2017). V. parahaemolyticus has been reported to cause enteritis when fishery products are ingested raw or after low temperature cooking (Feldhusen, 2000; Newton et al., 2012).

According to the foodborne illness statistics by the Ministry of Food and Drug Safety (MFDS, 2021) from 2010 to 2020, the number of cases of foodborne illness caused by V. parahaemolyticus was 225 and the number of patients was 1,524. Raw foods, such as sashimi and sushi, may be the primary cause of V. parahaemolyticus foodborne illness in South Korea (MFDS, 2015). A large-scale V. parahaemolyticus foodborne illness occurred due to raw oysters in 2003, resulting in a total of 91 patients (MFDS, 2013) and in 2017, at a bazaar of the Seoul Welfare Center in South Korea, cross-contamination occurred by cutting boards and knives from squid contaminated with V. parahaemolyticus, resulting in 273 patients (Jung, 2018).

In 2004, the 62 cases of V. parahaemolyticus infection in Alaska were caused by oysters, and the 177 cases of this infection in New York, Oregon, and Washington in the USA were caused by shellfish (McLaughlin et al., 2005; MMWR, 2006). Although no cases of V. parahaemolyticus foodborne illness have been reported from sea squirt consumption, there is a high likelihood of infection by it because sea squirt is eaten raw, like oysters.

Fishery products are those that are produced in seawater, which is inhabited by a mix of various microbial species. Additionally, these products are often exposed to a humid environment for a long time during processing and distribution, which actively maintains the growth and metabolism of contaminating microorganisms (Gram & Dalgaard, 2002). Sea squirts ingest viruses and bacteria from seawater by filter-feeding, and thereby accumulate these pathogens (Cliver, 1988; Grimes, 1991). Therefore, the standard growth conditions of sea squirts allow for V. parahaemolyticus contamination, posing a risk of foodborne illness upon consumption without sufficient washing. However, this risk has not been analyzed quantitatively.

Quantitative microbial risk assessment (QMRA) involves four stages: hazard identification, exposure assessment, hazard characterization, and risk characterization and is used to estimate the risk of foodborne illness (CAC, 1999). However, there have been very few studies that have assessed the risk of V. parahaemolyticus infection in fishery products, particularly tunicate.

Therefore, the objective of this study was to evaluate the risk of V. parahaemolyticus contamination in sea squirts by developing a Monte Carlo simulation model.

Materials and Methods

Examination of V. parahaemolyticus contamination in sea squirt

Sea squirt (Halocynthia roretzi) samples were purchased from online markets and markets in Seoul, Guri, Mokpo, and Tongyeong, South Korea. Twenty-five grams of sea squirt was placed into a sample bag purchased from 3M (Maplewood, MN, USA), and 225 mL alkaline peptone water (APW) purchased from Becton, Dickinson and Company (BD) (Franklin Lakes, NJ, USA) was placed in the same bag. The samples were then homogenized for 1 min (Wang et al., 2019) using a homogenizer purchased from Interscience (St. Nom-la-Bretèche, France). Homogenates were serially diluted with 9 mL APW, and 0.1 mL of the diluents were plated on thiosulfate citrate bile salt sucrose (TCBS) agar purchased from BD (Franklin Lakes) and incubated at 35°C for 24 h. The number of V. parahaemolyticus positive samples was fitted using Beta distribution to evaluate the prevalence of V. parahaemolyticus in sea squirt and estimate the initial contamination level (Vose, 1997).

Development of predictive models

Four V. parahaemolyticus strains, ATCC17802, ATCC27519, ATCC33844, and ATCC43996, that have toxin-producing genes (Lee et al., 2018) were cultured in 10 mL marine broth purchased from BD (Franklin Lakes) at 37°C for 24 h (Kim et al., 2019). Subcultures were prepared by adding 0.1 mL of the culture to 10 mL fresh marine broth at 37°C for 24 h. The subcultured strains were mixed and centrifuged at 1,912×g and 4°C for 15 min. The cell pellet was washed twice with phosphate-buffered (PBS pH 7.4: NaCl 8.0 g, NaHPO₄ 1.5 g, KH₂PO₄ 0.2 g, KCl 0.2 g in 1 L distilled water). The pellet was then diluted with PBS to 3.0–3.5 Log CFU/mL and served as the inoculum. One hundred and twenty sea squirt samples purchased from online markets were immersed in 2 L of the inoculum for 3 min, and the samples were then drained on a wicker tray for 10 min. The homogenization and enumeration steps of the samples were the same as the section of “Examination of V. parahaemolyticus in sea squirt”.

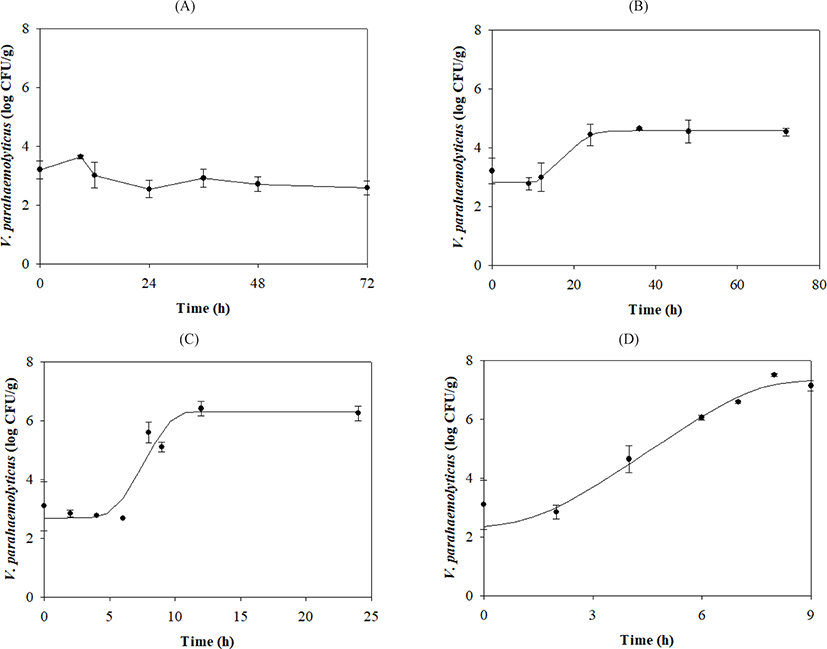
The cell count data were fitted to the Baranyi model (Baranyi & Roberts, 1994) to calculate maximum specific growth rate (μ_max; Log CFU/g/h), lag phase duration (LPD; h), initial bacterial cell count (N₀; Log CFU/g), final bacterial cell count (N_max; Log CFU/g), initial physiological state of the cells (h₀), and storage time (t), using the following formula:

N t = N 0 + μ max × A t − ln [exp (μ max × A t) − 1 exp (N max − N 0)] A t = t + 1 μ max ln (exp (− μ max) + q 0 1 + q 0) q 0 = 1 exp (h 0) − 1

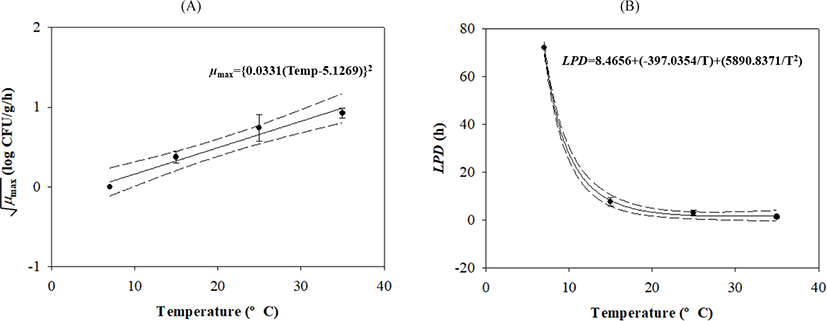
To analyze the effect of temperature on the kinetic parameters, μ_max values were analyzed using a square root equation [Y = {a_μ × (Temp – Temp_min)}²], and LPD values were analyzed using a polynomial equation [Y = (a / Temp) + (b / Temp²) + c].

To evaluate model performance, V. parahaemolyticus was inoculated in sea squirt as described above, and samples were stored at 10°C and 23°C. During storage, the V. parahaemolyticus concentration in sea squirts was quantified as described above. These values were compared with the predicted values calculated using the models developed at 10°C and 23°C, and the difference was analyzed by calculating the root mean square error (RMSE) (Baranyi et al., 1996).

R M S E = ∑ (p r e d i c t e d − o b s e r v e d) 2 n

Statistical analysis

μ_max and LPD values from primary models were analyzed using the general linear procedure with SAS® version 9.3 purchased from SAS Institute (Cary, NC, USA). Least square means among temperature data were compared using the t-test at α = 0.05.

Collection of distribution time and temperature data

The data for distribution temperature, time spent in transit to market, and time spent in home storage were collected by personal communication with a market employee. The data for food storage temperature at home was acquired from a study by Lee et al. (2015).

Estimation of amount and frequency of sea squirt consumption

To estimate the average amount of sea squirts consumed in Korea and to determine appropriate probability distributions, raw data from the Korea National Health and Nutrition Examination Surveys (KNHANES; KDCA, 2016) 2016 were inputted into @RISK version 6.0 software purchased from Palisade (Ithaca, NY, USA). To estimate the frequency of sea squirt consumption, the number of consumers was divided by the number of total respondents.

Determination of dose-response model

To determine the appropriate dose-response model for V. parahaemolyticus, all dose-response models in published literatures were reviewed.

Estimation of the probability of foodborne illness

To estimate the probability of foodborne illness per person per day for sea squirt consumption, a simulation model was developed in an Excel® spreadsheet purchased from Microsoft (Redmond, WA, USA) using data collected regarding prevalence, contamination level, duration and temperature of storage and transportation; predictive models; amount and frequency of consumption; and the dose-response model. The Monte Carlo simulation was generated using @RISK version 6.0, with 10,000 iterations.

Results and Discussion

Prevalence of V. parahaemolyticus in sea squirt

V. parahaemolyticus contamination was detected in 6 of 35 samples (17.1%). Due to the low detection frequency and levels of V. parahaemolyticus, the initial contamination level at the production stage was estimated by Beta distribution modeling [Beta (7, 30)] using the equation described by Sanaa et al. (2004). The initial contamination level of V. parahaemolyticus in sea squirt was calculated to be –2.1 Log CFU/g.

The predictive model to describe V. parahaemolyticus

V. parahaemolyticus growth gradually increased after lag phases, which decreased as the temperature increased (Table 1 and Fig. 1). Secondary models were developed to describe how temperature affects growth kinetic parameters during transport, display, and storage. The μ_max value was calculated as {0.0331 × (Temp – 5.1269)}² with R² = 0.839, and the LPD of the model was calculated as 8.4656 + (–397.0354 / Temp) + (5,890.8371 / Temp²) with R² = 0.997 (Fig. 2).

Table 1. Parameters calculated by the primary model for Vibrio parahaemolyticus growth in sea squirt during storage in 7°C, 15°C, 25°C, and 35°C

Kinetic parameters	Temperature (°C)
Kinetic parameters	7	15	25	35
μ _max	0.0 ± 0.0^C	0.2 ± 0.1^B	0.6 ± 0.4^A	0.9 ± 0.2^A
LPD	72.0 ± 0.0^A	8.6 ± 1.9^B	2.9 ± 2.1^C	1.3 ± 0.6^C
N ₀	3.3 ± 0.2	3.3 ± 0.4	3.0 ± 0.4	3.0 ± 0.7
N _max	3.5 ± 1.0	4.9 ± 0.8	6.4 ± 0.7	7.5 ± 0.4

Values are mean ± SD.

Values in the same row with different superscript letters are significantly different (p < 0.05).

μ_max, maximum growth rate; N₀, initial bacterial cell counts; N_max, final bacterial cell counts; LPD, lag phase duration.

Download Excel Table

Fig. 1. The primary model for Vibrio parahaemolyticus growth in sea squirt during storage at 7°C (A), 15°C (B), 25°C (C), and 35°C (D). •, observed data; —, fitted line.

Download Original Figure

Fig. 2. The µ_max (A) and LPD (B) values from the primary models and fitted line developed by the secondary model as a function of temperature for Vibrio parahaemolyticus in sea squirt. LPD, lag phase duration.

Download Original Figure

Distribution time and temperature

From producer to market

Surveys revealed that the average time taken for freshly harvested sea squirts to be transported to markets was 3.339 h or 5 h, depending on the distance. A time of 0 h was also observed in cases where sea squirts were carried directly to the market without additional transportation. Thus, an appropriate probability distribution was determined using Pert distribution using the following parameters: (0, 3.339, 5). Temperatures measured during transportation to markets were fitted with @RISK, and the Weibull distribution {Weibull [1.3219, 2.8404, Shift (3.1093), Truncate (1, 40)]} was used to generate a probability distribution.

During market display

Sea squirt samples were immediately displayed once they arrived at the market instead of being first stored in a warehouse. They were displayed for 0–48 h; thus, uniform distribution modeling (0, 48) was used. The display temperature ranged between –5.4°C and 18.1°C, and the probability distribution was calculated using Weibull distribution modeling {Weibull [2.2708, Shift (–8.4157), Truncate (–6, 18.1)]}.

From market to home

Sea squirts were consumed immediately or within 72 h after purchase. Therefore, we used uniform distribution (0, 72) for analysis. The probability distribution for home storage temperature was modeled using the LogLogistic distribution {LogLogistic [–29.283, 33.227, 26.666, Truncate (–5, 20)]}, as indicated by Lee et al. (2015).

Amount and frequency of consumption

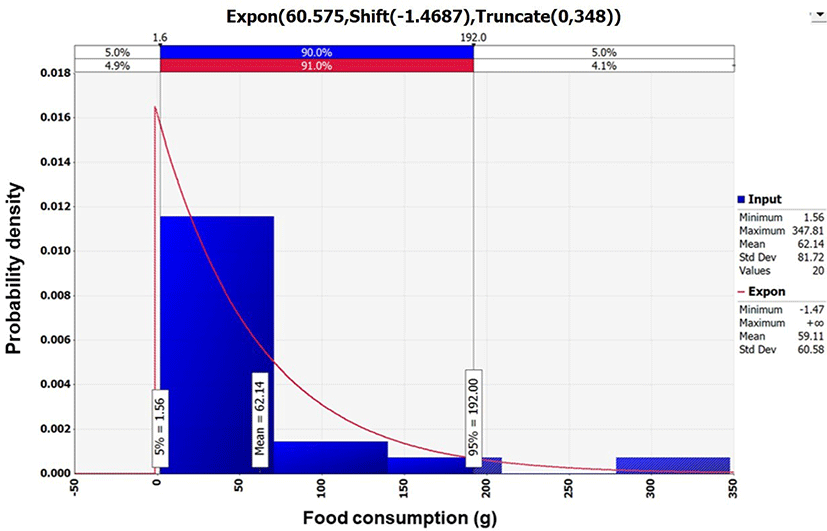
Data collected regarding the amount of sea squirt consumed were analyzed using @RISK, and Exponential distribution {Expon [60.575, Shift (–1.4687), Truncate (0, 348)]} was selected to generate a probability distribution (Fig. 3). According to the analysis by KNHANES, the average daily amount of sea squirt consumed was 62.14 g per day. Out of 7,042 total respondents, only 22 consumed sea squirts; therefore, the frequency of consumption was 0.28% in South Korea (KDCA, 2016).

Fig. 3. The probability distribution for intake of sea squirt obtained from the Korea National Health and Nutrition Examination Survey (KNHANES) 2016 with @RISK.

Download Original Figure

Dose-response model

To estimate the dose-response of V. parahaemolyticus, the Beta-Poisson model [P_illness = 1 – (1 + D / β)^–^α, α = 0.17, β = 1.18 × 10⁵] developed by Iwahori et al. (2010) and FAO & WHO (2011) was used. D is the number of ingested bacterial cells (CFU) and is calculated as 10^{final V. parahaemolyticus cell counts (Log CFU/g)} × daily amount of sea squirt consumed (g). α and β are fixed values representing the probability of a single V. parahaemolyticus cell causing foodborne illness.

The final V. parahaemolyticus cell count (Log CFU/g) was calculated as the total concentration from the initial contamination level through the transportation, display, and storage of sea squirt samples. The change in cell count was predicted using the developed predictive models.

Probability of V. parahaemolyticus foodborne illness

To calculate the probability of V. parahaemolyticus foodborne illness, a simulation model was prepared as shown in Table 2 using probability distributions for V. parahaemolyticus prevalence, temperature, time and quantity of consumption, and consumption frequency, as well as the predictive models and the dose-response model. The simulation indicated that the probability of V. parahaemolyticus infection following sea squirt consumption was 4.03 × 10⁻⁹ per person per day in Korea. This estimated risk is lower than that reported for raw oysters (Crassostrea gigas) in Brazil (4.7 × 10⁻⁴, 6.0 × 10⁻⁴, 4.7 × 10⁻⁴, and 3.1 × 10⁻⁴ per person per serving for spring, summer, fall, and winter, respectively) and for raw blood clams (Anadara broughtonii) in southern Thailand (5.6 × 10⁻⁴ per person per year) (Sobrinho et al., 2014; Yamamoto et al., 2008).

Table 2. Simulation models and formulas in Excel spreadsheet used to calculate the risk of Vibrio parahaemolyticus in sea squirt with @RISK

Input model	Unit	Variable	Formula	References
PRODUCT
Pathogens contamination level		PR	= RiskBeta (7, 30)	This research; Vose (1997)
V. parahaemolyticus concentration	CFU/g	C	= –LN (1–PR) / 25 g	Sanaa et al. (2004)
Initial contamination level	Log CFU/g	IC	= Log (C)	This research
TRANSPORTATION TO MARKET
Transportation
Transportation time	h	Time_trans	= RiskPert (0, 3.339, 5)	Personal communication; This research
Food temperature during transportation	°C	Temp_trans	= RiskWeibull (1.3219, 2.8404, RiskShift (3.1093), Risktruncate (1, 40))	Personal communication; This research
Growth
		h₀	= average (growth rate × lag phase duration), Fixed 1.14	This research; Baranyi & Roberts (1994)
	Log CFU/g	Y₀	= average (Y₀i), Fixed 3.1	This research; Baranyi & Roberts (1994)
	Log CFU/g	Y_end	= average (Y_endi), Fixed 5.6	This research; Baranyi & Roberts (1994)
		ln(q)	= LN (1 / (EXP (h₀) – 1))	This research; Baranyi & Roberts (1994)
Growth rate	Log CFU/g/h	GR_trans	= IF (Temp_trans > 4.9515, 0.0330 × (Tempt_rans–4.9515))²), 0)	This research; Baranyi & Roberts (1994)
V. parahaemolyticus growth model	Log CFU/g	C1	= IC + 1 / (1 + EXP (–ln(q))) × (1 – 10^{−\|Y0–Yend\|} / LN(10)) × GR_trans × Time_trans	This research; Baranyi & Roberts (1994)
MARKET
Market display
Display time	h	Time_Mark-dis	= RiskUniform(0,48)	Personal communication; This research
Food temperature during display	°C	Temp_Mark-dis	= RiskWeibull (2.2708, 21.394, RiskShift (–8.4157), RiskTruncate (–6, 18.1))	Personal communication; This research
Growth
		h₀	= average(growth rate × lag phase duration), Fixed 1.14	This research; Baranyi & Roberts (1994)
	Log CFU/g	Y₀	= average(Y₀i), Fixed 3.1	This research; Baranyi & Roberts (1994)
	Log CFU/g	Y_end	= average(Y_endi), Fixed 5.6	This research; Baranyi & Roberts (1994)
		ln(q)	= LN (1 / (EXP(h₀) – 1))	This research; Baranyi & Roberts (1994)
Growth rate	Log CFU/g/h	GR_Mark-dis	= IF(Temp_Mark-dis > 4.9515, 0.0330 × (Temp_Mark-dis – 4.9515))²), 0)	This research; Baranyi & Roberts (1994)
V. parahaemolyticus growth model	Log CFU/g	C2	= C1 + 1 / (1 + EXP (-ln(q))) × (1 – 10^{−\|Y0–Yend\|} / LN(10)) × GR_Mark-dis × Time_Mark-dis	This research; Baranyi & Roberts (1994)
HOME
Home storage
Storage time	H	Time_Home-st	= RiskUniform (0, 72)	Personal communication; This research
Food temperature during storage	°C	Temp_Home-st	= RiskLogLogistic (–29.283, 33.227, 26.666, RiskTruncate (–5, 20))	Lee et al. (2015)
Growth
		h₀	= average (growth rate × lag phase duration), Fixed 1.14	This research; Baranyi & Roberts (1994)
	Log CFU/g	Y₀	= average (Y₀i), Fixed 3.1	This research; Baranyi & Roberts (1994)
	Log CFU/g	Y_end	= average (Y_endi), Fixed 5.6	This research; Baranyi & Roberts (1994)
		ln(q)	= LN (1 / (EXP (h₀)–1))	This research; Baranyi & Roberts (1994)
Growth rate	Log CFU/g/h	GR_Home-st	= IF (Temp_Home-st > 4.9515, 0.0330 × (Temp_Home-st – 4.9515))²), 0)	This research; Baranyi & Roberts (1994)
V. parahaemolyticus growth model	Log CFU/g	C3	= C2+1 / (1 + EXP (–ln(q))) × (1–10^{−\|Y0–Yend\|} / LN(10)) GR_Home-st × Time_Home-st	This research; Baranyi & Roberts (1994)
CONSUMING
Daily consumption amount	g	Consump	= RiskExpon (60.575, RiskShift (–1.4687), RiskTruncate (0, 348))	KDCA (2016)
Daily consumption frequency	%	ConFre	Fixed 0.28	KDCA (2016)
		CF(0)	= 1 – 0.28 / 100	KDCA (2016)
		CF(1)	= 0.28 / 100	KDCA (2016)
		CF	= RiskDiscrete ({0, 1}, {CF (0), CF (1)})	KDCA (2016)
		Amount	= IF (CF = 0, 0, Consump)	KDCA (2016)
DOSE-RESPONSE
V. parahaemolyticus amount	CFU	D	= 10^C3 × Amount
Parameter of α		α	Fixed 0.17	Iwahori et al. (2010); FAO & WHO (2011)
Parameter of β		β	Fixed 1.18 × 10⁵	Iwahori et al. (2010); FAO & WHO (2011)
RISK
Probability of illness/person/day		Risk	= 1 – (1 + D/β)^−α	Iwahori et al. (2010); FAO & WHO (2011)

Download Excel Table

According to Lee et al. (2015) and Lee et al. (2016) studies, the mean probability of Clostridium perfringens and Staphylococcus aureus foodborne illness for processed cheese were 3.58 × 10⁻¹⁴ and 2.24 × 10⁻⁹ per person per day, respectively. As described in Jung et al. (2017), the mean probability of Campylobacter foodborne illness in raw beef offal for home consumption was 1.56 × 10⁻⁵ per person per day.

Therefore, the probability of foodborne illness by consuming sea squirt contaminated with V. parahaemolyticus is higher than that of C. perfringens and S. aureus foodborne illness from having processed cheese, and lower than that of Campylobacter foodborne illness from consuming raw beef offal.

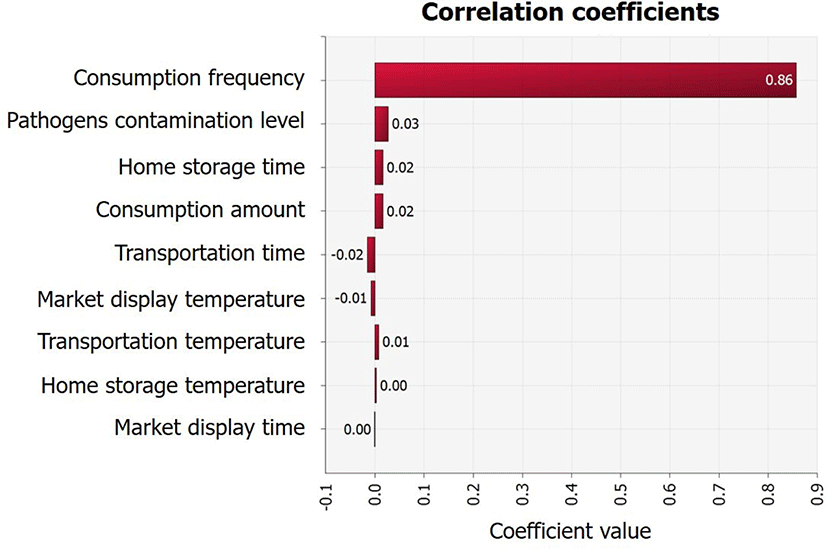
Although the average initial V. parahaemolyticus contamination level in sea squirts was as low as -2.1 Log CFU/g, the probability of infection was calculated separately because the contamination levels were found to increase from the initial concentration (IC) stage to stages C1 (V. parahaemolyticus concentration from producer to market), C2 (V. parahaemolyticus concentration from during market display), and C3 (V. parahaemolyticus concentration from market to home) (Fig. 4). This increase was influenced by temperature and duration of transit, as demonstrated by the correlation coefficient (Fig. 5). In addition, the correlation coefficient indicated that the amount and frequency of consumption, as well as pathogen contamination levels increase the probability of foodborne illness (Fig. 5).

Fig. 4. Growth of Vibrio parahaemolyticus by domestic distribution in sea squirt. IC, initial concentration; C1, concentration from producer to market; C2, concentration from during market display; C3, concentration from market to home.

Download Original Figure

Fig. 5. Correlation coefficient values for risk factors, affecting the probability of Vibrio parahaemolyticus foodborne illness per person per day caused by sea squirt consumption.

Download Original Figure

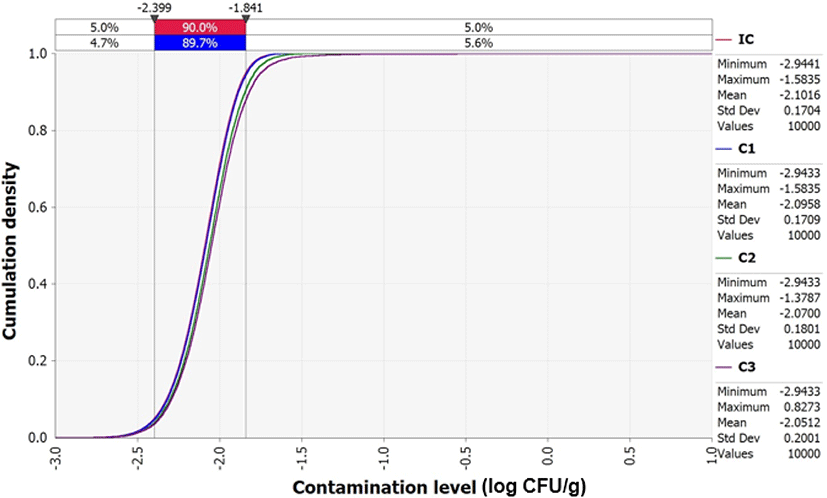
In conclusion, sea squirt samples had relatively low levels of V. parahaemolyticus contamination. The low amount and frequency of sea squirts consumption in South Korea were the main factors that decreased the probability of V. parahaemolyticus foodborne illness. However, according to the predictive models developed in this study, cell counts of V. parahaemolyticus also increased over time, which may in turn increase the probability of V. parahaemolyticus infection if the contaminated sea squirts are distributed or stored for long periods and at elevated temperatures. According to the results of this study, –2.1 Log CFU/g of V. parahaemolyticus contamination level was consumed immediately after harvest of sea squirt, and –1.8 Log CFU/g of V. parahaemolyticus contamination level was consumed approximately 63 h after harvest. Therefore, it is recommended to consume sea squirt as soon as possible as the risk continues to increase immediately after exposure to V. parahaemolyticus.

Competing interests

No potential conflict of interest relevant to this article was reported.

Funding sources

This research was supported by a grant (17162MFDS035) from Ministry of Food and Drug Safety in 2018.

Acknowledgements

Not applicable.

Availability of data and materials

All datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.

Ethics approval and consent to participate

This article does not require IRB/IACUC approval because there are no human and animal participants.

References

Baranyi J, Roberts TA. A dynamic approach to predicting bacterial growth in food. Int J Food Microbiol. 1994; 23:277-94

Baranyi J, Ross T, McMeekin TA, Roberts TA. Effects of parameterization on the performance of empirical models used in ‘predictive microbiology’. Food Microbiol. 1996; 13:83-91

Codex Alimentarius Commission [CAC]. Principles and guidelines for the conduct of microbiological risk assessment [Internet]. 1999[cited 2019 Aug 31]http://www.fao.org/3/y1579e/y1579e05.htm

Feldhusen F. The role of seafood in bacterial foodborne diseases. Microbes Infect. 2000; 2:1651-60

Food and Agriculture Organization of the United Nations [FAO]. The state of world fisheries and aquaculture 2016: contributing to food security and nutrition for all. Rome: FAO. 2016; p p. 200.

Food and Agriculture Organization of the United Nations [FAO]. The state of world fisheries and aquaculture 2018: meeting the sustainable development goals. Rome: FAO. 2018; p p. 227.

Food and Agriculture Organization of the United Nations [FAO], World Health Organization [WHO]. Risk assessment of Vibrio parahaemolyticus in seafood [Internet]. 2011[cited 2019 Aug 10]http://www.fao.org/3/i2225e/i2225e00.pdf

Food and Drug Administration [FDA]. Bad bug book: handbook of foodborne pathogenic microorganisms and natural toxins [Internet]. 2017[cited 2019 Sep 6]https://www.fda.gov/media/83271/download

Gram L, Dalgaard P. Fish spoilage bacteria-problems and solutions. Curr Opin Biotechnol. 2002; 13:262-66

10.

Grimes DJ. Ecology of estuarine bacteria capable of causing human disease: a review. Estuaries. 1991; 14:345-60

11.

Iwahori J, Yamamoto A, Suzuki H, Yamamoto T, Tsutsui T, Motoyama K, et al. Quantitative risk assessment of Vibrio parahaemolyticus in finfish: a model of raw horse mackerel consumption in Japan. Risk Anal. 2010; 30:1817-32

12.

Jung J, Lee J, Lee H, Lee S, Kim S, Ha J, et al. Quantitative microbial risk assessment for Campylobacter foodborne illness in raw beef offal consumption in South Korea. J Food Prot. 2017; 80:609-18

13.

Jung SW. A foodborne outbreak of gastroenteritis caused by Vibrio parahaemolyticus associated with cross-contamination from squid in Korea. Epidemiol Health. 2018; 40:e2018056

14.

Kim HJ, Sujiwo J, Kim HJ, Jang A. Effects of dipping chicken breast meat inoculated with Listeria monocytogenes in lyophilized scallion, garlic, and kiwi extracts on its physicochemical quality. Food Sci Anim Resour. 2019; 39:418-29

15.

Kim JH, Kim MJ, Lee JS, Kim KH, Kim HJ, Heu MS, Kim JS. Development and characterization of sea squirt Halocynthia roretzi Sikhae. Kor J Fish Aquat Sci. 2013; 46:27-36

16.

Korea Centers for Disease Control and Prevention [KDCA]. Korea health statistics 2016 [Internet]. Korean National Health and Nutrition Examination Surveys [KNHANES]. 2016[cited 2019 Aug 20]https://knhanes.cdc.go.kr/knhanes/sub03/sub03_02_02.do

17.

KOSTAT [Statistics Korea]. Fishery product consumption (per person per year) [Internet]. 2019[cited 2019 Sep 28]http://www.index.go.kr/potal/stts/idxMain/selectPoSttsIdxSearch.do?idx_cd=1317&stts_cd=131701&freq=Y

18.

Lee H, Kim K, Choi KH, Yoon Y. Quantitative microbial risk assessment for Staphylococcus aureus in natural and processed cheese in Korea. J Dairy Sci. 2015; 98:5931-45

19.

Lee H, Lee S, Kim S, Lee J, Ha J, Yoon Y. Quantitative microbial risk assessment for Clostridium perfringens in natural and processed cheeses. Asian-Australas J Anim Sci. 2016; 29:1188-96

20.

Lee J, Lee H, Lee S, Kim S, Ha J, Choi Y, Oh H, et al. Quantitative microbial risk assessment for Campylobacter jejuni in ground meat products in Korea. Food Sci Anim Resour. 2019; 39:565-75

21.

Lee Y, Choi Y, Lee S, Lee H, Kim S, Ha J, et al. Occurrence of pathogenic Vibrio parahaemolyticus in seafood distribution channels and their antibiotic resistance profiles in S. Korea. J Appl Microbiol. 2018; 68:128-33

22.

McLaughline JB, DePaola A, Bopp CA, Martinek KA, Napolilli NP, Allison CG, et al. Outbreak of Vibrio parahaemolyticus gastroenteritis associated with Alaskan oysters. N Engl J Med. 2005; 353:1463-70

23.

Ministry of Food and Drug Safety [MFDS]. Pathogenic microorganism profile [Internet]. 2013[cited 2021 Jan 10]https://mfds.go.kr/brd/m_228/view.do?seq=15129&srchFr=&srchTo=&srchWord=&srchTp=&itm_seq_1=0&itm_seq_2=0&multi_itm_seq=0&company_cd=&company_nm=&page=7

24.

Ministry of Food and Drug Safety [MFDS]. Microbial risk profile [Internet]. 2015[cited 2019 Oct 20]https://mfds.go.kr/brd/m_227/view.do?seq=25230&srchFr=&srchTo=&srchWord=&srchTp=&itm_seq_1=0&itm_seq_2=0&multi_itm_seq=0&company_cd=&company_nm=&page=13

25.

Ministry of Food and Drug Safety [MFDS]. Foodborne illness statistics [Internet]. 2021[cited 2021 Jan 10]https://www.foodsafetykorea.go.kr/portal/healthyfoodlife/foodPoisoningStat.do?menu_no=3724&menu_grp=MENU_NEW02

26.

Newton A, Kendall M, Vugia DJ, Henao OL, Mahon BE. Increasing rates of vibriosis in the United States, 1996-2010: review of surveillance data from 2 systems. Clin Infect Dis. 2012; 54:S391-95

27.

Organization for Economic Cooperation and Development [OECD], Food and Agriculture Organization of the United Nations [FAO]. OECD-FAO agricultural outlook 2018-2027 [Internet]. 2018[cited 2020 Apr 30]http://www.fao.org/3/I9166EN/I9166EN.pdf

28.

Sanaa M, Coroller L, Cerf O. Risk assessment of listeriosis linked to the consumption of two soft cheeses made from raw milk: camembert of normandy and brie of Meaux. Risk Anal. 2004; 24:389-99

29.

Sobrinho PS, Destro MT, Franco BD, Landgraf M. A quantitative risk assessment model for Vibrio parahaemolyticus in raw oysters in Sao Paulo state, Brazil. Int J Food Microbiol. 2014; 180:69-77

30.

Vibrio parahaemolyticus infections associated with consumption of raw shellfish-three states, 2006. MMWR [Morbidity and Mortality Weekly Report]. 2006[cited 2020 Apr 26]https://www.cdc.gov/mmwr/preview/mmwrhtml/mm55d807a1.htm

31.

Vose DJ. Risk analysis in relation to the importation and exportation of animal products. Rev Sci Tech. 1997; 16:17-29

32.

Wang T, Guo H, Zhang H, Ren F, Zhang M, Ge S, et al. Dynamics of bacterial communities of lamb meat packaged in air and vacuum pouch during chilled storage. Food Sci Anim Resour. 2019; 39:209-21

33.

Yamamoto A, Iwahori J, Vuddhakul V, Charernjiratragul W, Vose D, Osaka K. Quantitative modeling for risk assessment of Vibrio parahaemolyticus in bloody clams in southern Thailand. Int J Food Microbiol. 2008; 124:70-78